Relación uno a muchos 1:N
- Significa que cada elemento de una entidad del tipo A
puede relacionarse con cualquier cantidad de elementos de
una entidad del tipo B, y un elemento de una entidad del
tipo B solo puede estar relacionado con un elemento de una
entidad del tipo A. Su representación gráfica es la
siguiente: Nótese en este caso que el extremo punteado de la
flecha de la relación de A y B, indica un elemento de A
conectado a muchos de B.

Ejemplo cardinalidad 1:N

- Muchos a muchos N:M
-
Establece que cualquier cantidad de
elementos de una entidad del tipo A pueden estar
relacionados con cualquier cantidad de elementos de una
entidad del tipo B. El extremo de la flecha que se encuentra
punteada indica el «varios» de la relación.

Ejemplo cardinalidad N:M

La Participación de una entidad
La participación de una entidad
también se conoce como cardinalidad de la entidad dentro de una
relación. Una misma entidad puede tener distinta cardinalidad
dentro de distintas relaciones. Para obtener la participación,
se debe fijar una ocurrencia concreta de una entidad y averiguar
cuántas ocurrencias de la otra entidad le corresponden como
mínimo y como
máximo.
Después realizar lo mismo en el otro
sentido. Estas ocurrencias mínimas y máximas (llamadas también
participación de una entidad) se representarán entre paréntesis
y con letras minúsculas en el lado de la relación opuesto a la
entidad cuyas ocurrencias se fijan.
Para determinar la cardinalidad nos quedamos con las participaciones
máximas de
ambas y se representan con letras mayúsculas separadas por dos
puntos junto al símbolo de la relación. Veamos algunos ejemplos:
Ejemplo 1

Un conductor
«conduce» como
mínimo 1 coche y como máximo 1 coche → Participación (1,1) y se
pone en el lado opuesto a CONDUCTOR, es decir, junto a COCHE.
Un
coche «es conducido» como mínimo por 1 conductor y como máximo
por 1 conductor → Participación (1,1) y se pone en el lado
opuesto a COCHE, es decir, junto a CONDUCTOR. Para determinar la
cardinalidad nos quedamos con las dos participaciones máximas.
Es decir → 1:1.
Ejemplo 2

Un cliente «compra» como mínimo
1 coche y como máximo puede comprar más de un coche, es decir,
varios coches. Ese varios se representa con la letra «n» →
Participación (1,n)) y se pone en el lado opuesto a CLIENTE, es
decir, junto a COCHE.
Un coche «es comprado» como mínimo por 1
cliente y como máximo por 1 cliente → Participación (1,1) y se
pone en el lado opuesto a COCHE, es decir, junto a CLIENTE.
Para
determinar la cardinalidad nos quedamos con las dos
participaciones máximas y la «n» se pone en mayúsculas «N». Es
decir → 1:N.
1:N se lee Un cliente
puede comprar muchos coches
Ejemplo 3
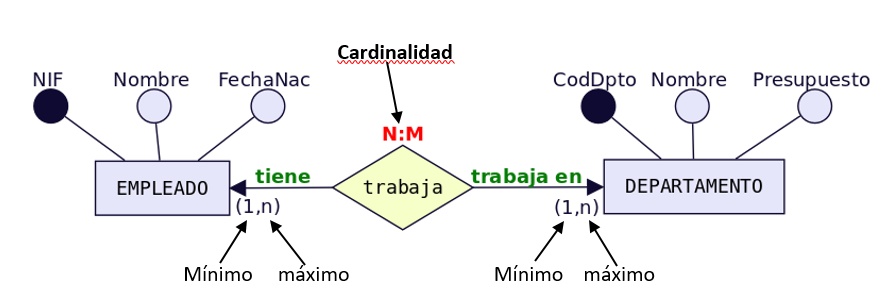
Un empleado «trabaja» como
mínimo 1 departamento y como máximo puede trabajar en varios.
Ese varios se representa con la letra «n» → Participación(1,n))
y se pone en el lado opuesto a EMPLEADO, es decir, junto a
DEPARTAMENTO.
Un departamento «tiene» como mínimo por 1 empleado
y como máximo puede tener varios → Participación (1,n) y se pone
en el lado opuesto a DEPARTAMENTO, es decir, junto a EMPLEADO.
Para determinar la cardinalidad nos quedamos con las dos
participaciones máximas y la «n» se pone en mayúsculas «N» y
para diferenciar el otro «varios» en lugar de «N» ponemos «M»
(Igual que cuando en matemáticas había dos variables no se ponía
x e x sino x e y). Es decir → N:M.
N:M.
se lee muchos empleados trabajan en muchos
departamentos
Atributos propios de una relación
Las relaciones también pueden
tener atributos, se les denominan atributos propios. Son
aquellos atributos cuyo valor sólo se puede obtener en la
relación, puesto que dependen de todas las entidades que
participan en la relación. Veamos un ejemplo.
Ejemplo:
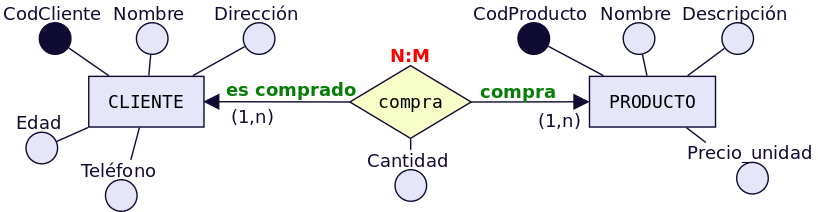
Tenemos la relación «Compra»
entre cliente y producto. Así un cliente puede comprar uno o
varios productos, y un producto puede ser comprado por uno o
varios clientes. Encontramos una serie de atributos propios de
cada una de las entidades [CLIENTE (Cod_Cliente, Nombre,
Dirección, edad, teléfono) y PRODUCTO (Cod_Producto, Nombre,
Descripción, Precio_Unidad)], pero también podemos observar como
el atributo «Cantidad» es un atributo de la relación. ¿Por qué?
Pues porque un mismo cliente puede comprar distintas cantidades
de distintos productos y un mismo producto puede ser comprado en
distintas cantidades por distintos clientes. Es decir el
atributo cantidad depende del cliente y del producto de que se
traten.
Relaciones de dependencia: Entidades Fuertes y
Entidades Débiles
Al definir las entidades
hablamos de dos tipos de ellas: fuertes y débiles. Una entidad
débil está unida a una entidad fuerte a través de una relación
de dependencia. Hay dos tipos de relaciones de dependencia:
Dependencia en
existencia Se produce cuando una entidad
débil necesita
de la presencia de una fuerte para existir. Si desaparece la
existencia de la entidad fuerte, la de la débil carece de
sentido. Se representa con una barra atravesando el rombo y la
letra E en su interior. Son relaciones poco frecuentes.
Ejemplo:
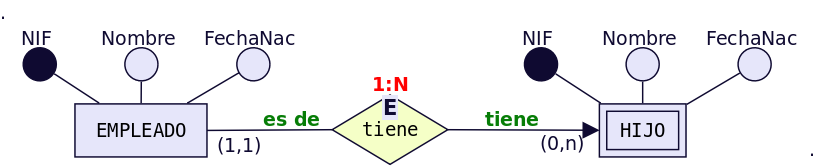
En la figura se muestra el caso
de que un empleado puede tener ninguno, uno o varios hijos, por
lo que los datos de los hijos deben sacarse en una entidad
aparte, aunque siguen siendo datos propios de un empleado. Si se
eliminase un registro de un empleado, no tendría sentido seguir
manteniendo en la base datos la información sobre sus hijos.
Dependencia en
identificación Se produce cuando una entidad débil
necesita de la fuerte para identificarse. Por sí sola la débil
no es capaz de identificar de manera unívoca sus ocurrencias. La
clave de la entidad débil se forma al unir la clave de la
entidad fuerte con los atributos identificadores de la entidad
débil.
Ejemplo:
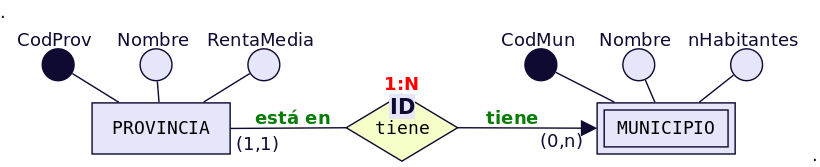
En la figura se observa que la
provincia tiene uno o varios municipio y que un municipio
pertenece a una sola provincia. Ahora bien si lo que identifica
a los municipios es el código que aparece en el código postal,
se tiene que las dos primeras cifras corresponden al código de
la provincia y las tres últimas al del municipio.
Por ejemplo,
el C.P de Écija es 41400, dónde 41 es el código de la provincia
y 400 el del municipio. De esta forma, habrá distintos
municipios con código 400 en distintas provincias. Uno de estos
municipios se distinguirá del resto al anteponerle las dos
primeras cifras correspondientes al código de la provincial.
Símbolos de exclusividad o inclusividad entre
relaciones
Otros símbolos usados en el
modelo E/R son los siguientes:
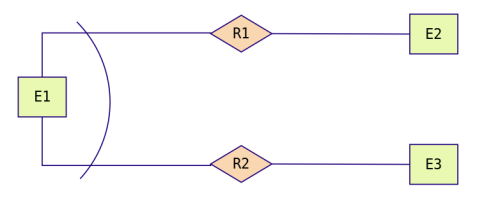
Restricción de
exclusividad entre dos tipos de relaciones R1 y R2
respecto a la entidad E1. Significa que E1 está relacionada, o
bien con E2 o bien con E3, pero no pueden darse ambas relaciones
simultáneamente.
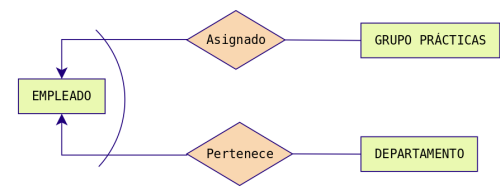
Ejemplo: Un empleado puede estar
en una empresa, o bien realizando prácticas, en cuyo caso está
asignado a un grupo de prácticas y no pertenece a ningún
departamento en concreto. O bien puede ser empleado en plantilla
y en este caso pertenece a un departamento.
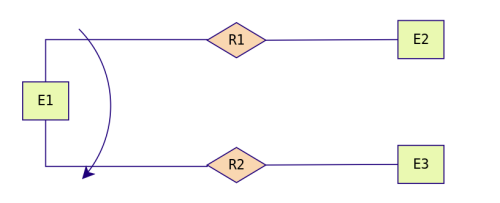
Restricción de
inclusividad entre dos tipos de relaciones R1 y R2
respecto a la entidad E1. Para que la entidad E1 participe en la
relación R2 debe participar previamente en la relación R1.
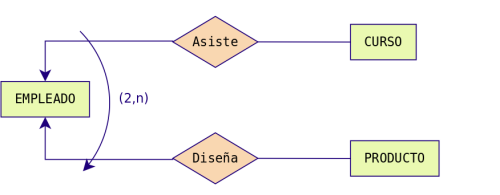
Ejemplo: Para que un empleado
pueda trabajar como diseñador de productos debe haber asistido,
al menos, a dos cursos.
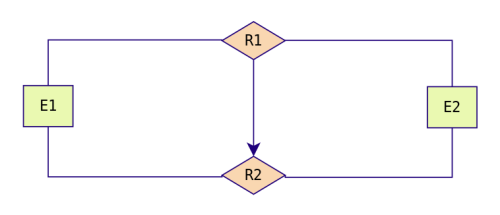
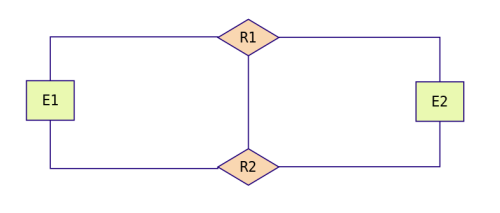
Restricción de exclusión entre
dos tipos de relaciones R1 y R2. Significa que E1 está
relacionada con E2 bien mediante R1, o bien mediante R2 pero que
no pueden darse ambas relaciones simultáneamente.
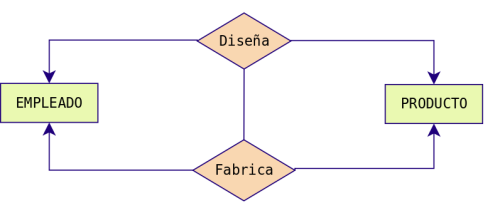
Ejemplo: Los empleados, en
función de sus capacidades, o son diseñadores de productos o son
operarios y los fabrican, no es posible que ningún empleado sea
diseñador y fabricante a la misma vez.
Restricción de inclusión entre
dos tipos de relaciones R1 y R2. Para que la entidad E1
participe en la relación R2 con E2 debe participar previamente
en la relación R1.
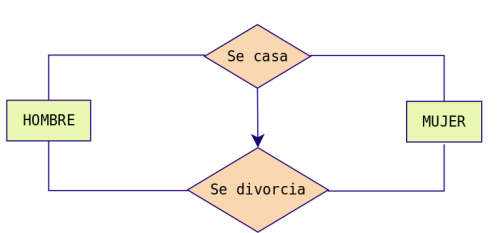
Ejemplo: Para que un hombre se
divorcie de una mujer, previamente ha de haberse casado con
ella.